机器学习-第一周
什么是机器学习?
第一个机器学习的定义来自于Arthur Samuel。
他定义机器学习为,在进行特定编程的情况下,给予计算机学习能力的领域。
Samuel的定义可以回溯到50年代,他编写了一个西洋棋程序。
这程序神奇之处在于,编程者自己并不是个下棋高手。
但因为他太菜了,于是就通过编程,让西洋棋程序自己跟自己下了上万盘棋。
通过观察哪种布局(棋盘位置)会赢,哪种布局会输,久而久之,
这西洋棋程序明白了什么是好的布局,什么样是坏的布局。然后就牛逼大发了,
程序通过学习后,玩西洋棋的水平超过了Samuel。这绝对是令人注目的成果。
机器学习的类型大致可以分为三种:
1、有监督学习:有类别标签的学习,基于训练样本的输入、输出训练得到最优模型,再使用该模型预测新输入的输出
2、无监督学习
3、强化学习
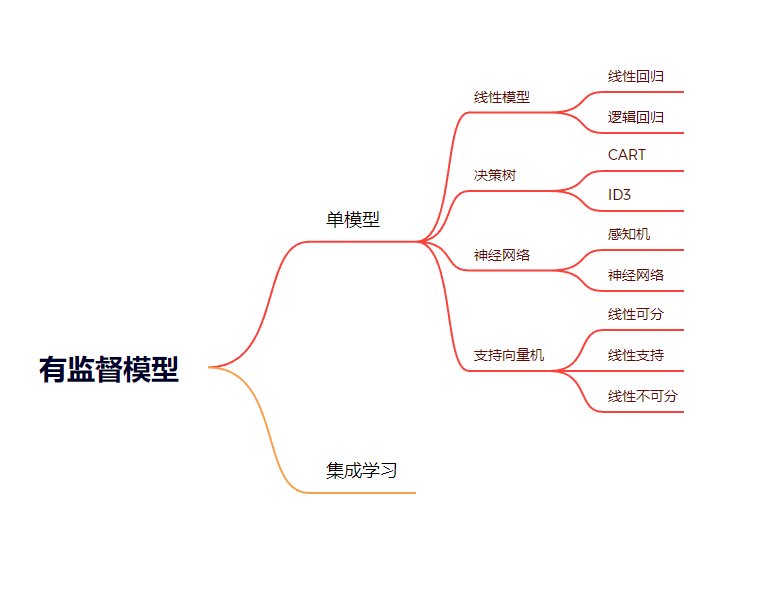
利用有监督学习解决的问题大致上可以被分为两类:
分类问题:预测某一样本所属的类别(离散的)。比如给定一个人的数据结构,包括:身高,年龄,体重等信息,然后判断是否健康。
回归问题:预测某一样本的所对应的实数输出(连续的)。比如预测某一地区人的平均身高。
代表算法:决策树、朴素贝叶斯、逻辑回归、KNN、SVM、神经网络、随机森林、AdaBoost、遗传算法;
1、线性回归算法
在机器学习当中,我们有一个变量X的集合用来决定输出变量Y。在输入变量X和输出变量Y之间存在着某种关系。机器学习的目的就是去量化这种关系。
在线性回归里,以三个输入维度A、B、C来预测P为例,我们的线性方程可以写为:
F=W1∗A+W2∗B+W3∗C
假设我们知道P的值其实就是与A的值有关,与B、C毫无关系,线性方程的计算结果F是三个维度的加权和,想要使F与P最接近,只需要让线性方程中B、C这两个加项对结果影响最小即可。
这个好办,只要使这两项的权值最小,也就是W2和W3的值为0就可以了。
这里实际上体现了一种假设,就是待预测的结果与输入的某个或某几个维度相关,而调整权值的目的就是使得与预测结果相关度高的权值越高,确保相关维度的值对最终加权和的贡献越大,反之权值越低,贡献越小。
线性回归的算法原理
拟合
对于一个线性回归问题,也就是说,这里的方程就是一个线性方程,相应的数据集点也一定是根据线性排布的,那么,我们要做的就是不断调整线性方程的两个变量,作出一条能够一一通过这些点的直线,也就是拟合。这个能够拟合数据集点的线性方程,就是我们要找的方程。
那怎样调整权值才能最终达到拟合数据的目标? 这里涉及到机器学习最核心的概念:在错误中学习。
这中间一环需要分两个步骤:首先知道偏离了多少,然后向减少偏差的方向调整权值。这个不断修正的过程就是机器学习中的“学习”,有一点像画画的时候勾勒人物轮廓一样。 具体来说需要经过以下两个步骤:
偏差度量:我们不仅要知道偏了,还要知道偏了多少,找到目标和实际的偏差距离。在机器学习中我们使用“损失函数”来度量偏差的距离。
权值调整:调整权值要解决两个细节问题,即权值是要增加还是减少、增加多少或者减少多少。
这两个问题都可以直接使用现成的数学工具进行解决,机器学习中将这些数学工具称为“优化方法”。
实例
有这样一组数据,
1 | data = [[5.05, 5.69], [4.92, 6.61], [4.67, 5.48], [4.54, 6.11], [4.26, 6.39], |
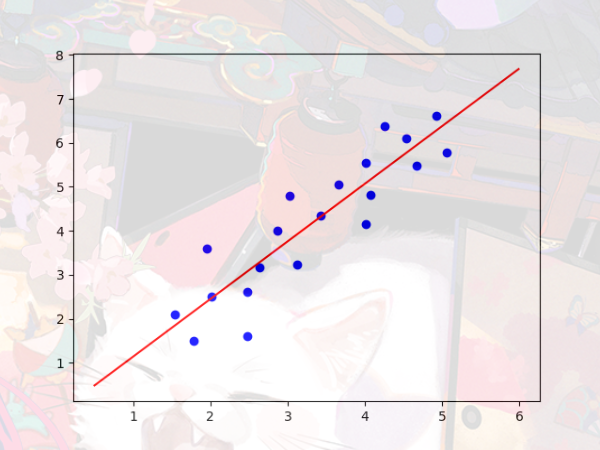
它的图像画出来是这样的散点图:
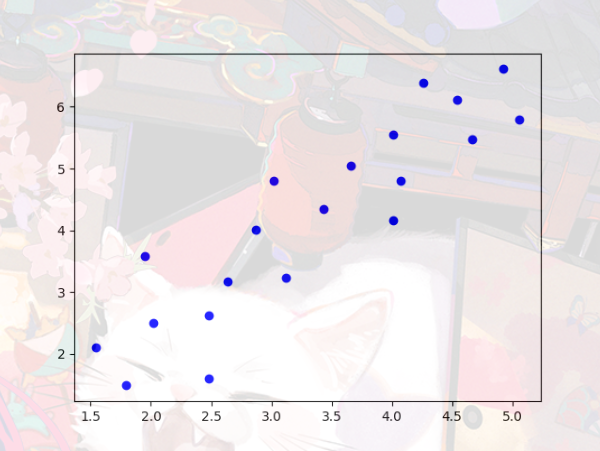
接下来我们引入两个数据分析用到的库
1 | import matplotlib.pyplot as plt |
我们使用最小二乘法解决这一个问题,我们先来看一下公式
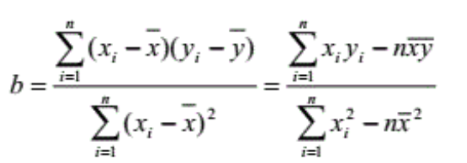
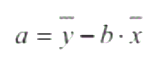
1 | def linear_plot(): |
最后我们得出的拟合方程和图像
y=1.31x-0.17
2. 逻辑回归算法
逻辑回归预测的是离散的值(比如一个学生CB有没有挂科,是:0,否:1)。
逻辑回归最适用于二分类(数据只分为两类,Y=0或1,一般用1作为默认的类)。
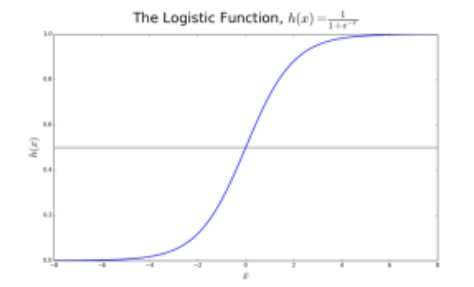
我们称其为逻辑回归(logistic regression)是因为我们的转换函数采用了logistic函数 (h(x)=1/(1+e的-x次方)),也叫sigmoid函数
在逻辑回归中,我们首先得到的输出是连续的默认类的概率p(0到1)。转换函数 (h(x)=1/(1+e的-x次方))的值域便是(0,1)。我们对该函数设置一个域值t。若概率p>t,则预测结果为1。
因此,逻辑回归的目标便是训练数据找到适当的参数的值,使得预测的输出和实际的输出最小。
这是CSDN的一篇文章,里面对于逻辑回归算法有非常详细的教程